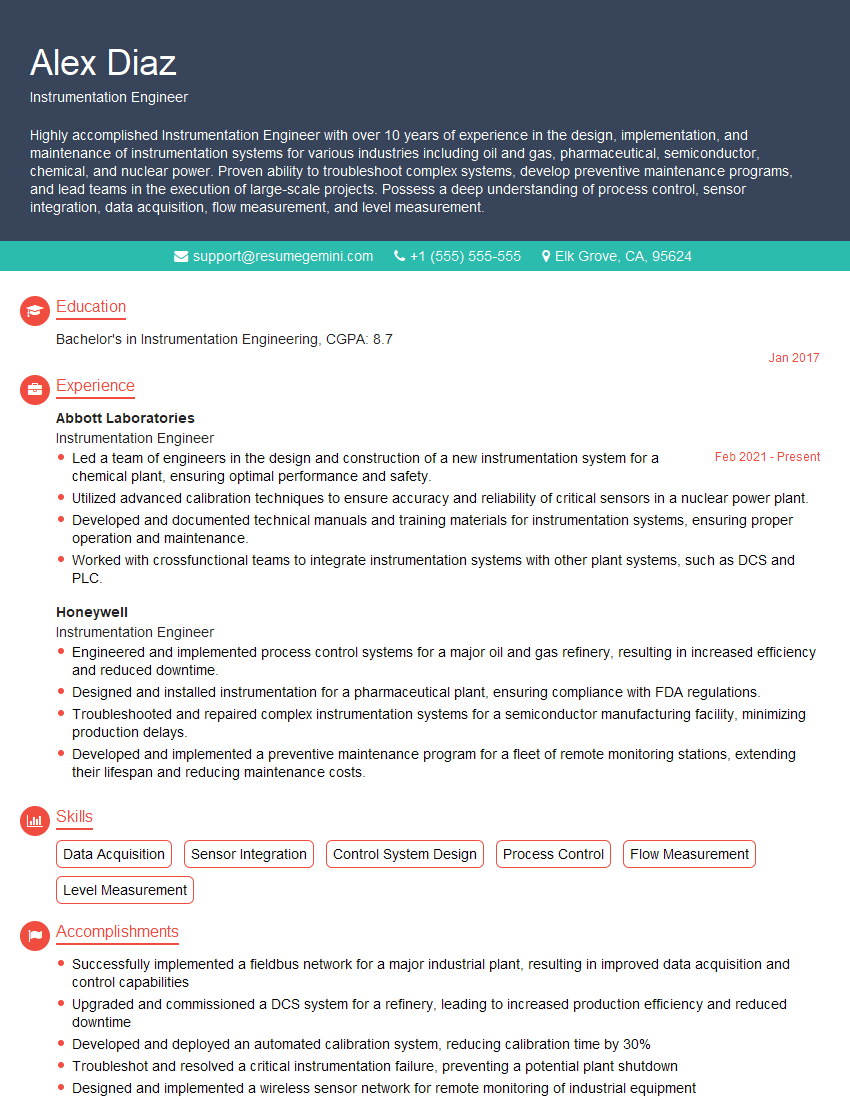
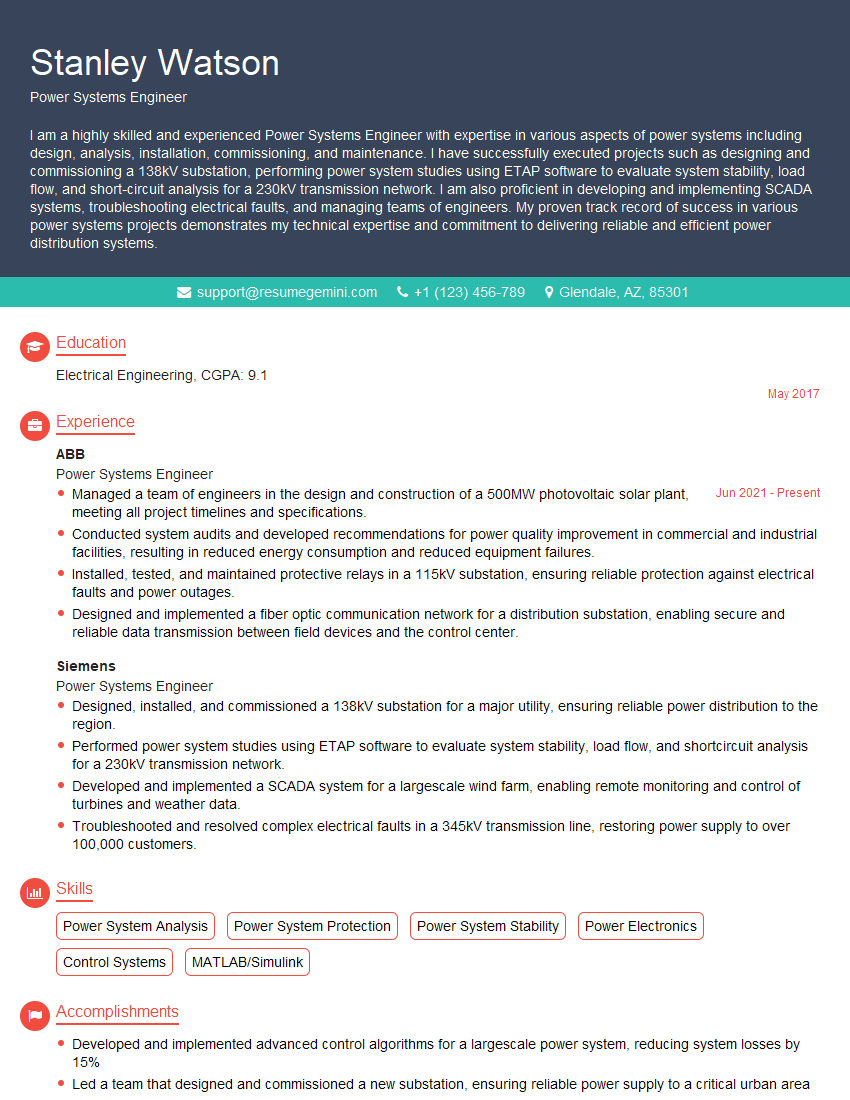
Every successful interview starts with knowing what to expect. In this blog, we’ll take you through the top Transmission Line Theory interview questions, breaking them down with expert tips to help you deliver impactful answers. Step into your next interview fully prepared and ready to succeed.
Questions Asked in Transmission Line Theory Interview
Q 1. Explain the concept of characteristic impedance and its significance in transmission line analysis.
Characteristic impedance (Z0) is a fundamental parameter of a transmission line, representing the ratio of voltage to current of a wave propagating along the line in the absence of reflections. It’s analogous to the resistance you’d encounter in a simple DC circuit, but for AC signals traveling along a line with distributed inductance, capacitance, resistance, and conductance. Think of it as the line’s inherent ‘resistance’ to the flow of electromagnetic energy.
Its significance lies in its role in determining how efficiently power is transferred along the line. When the impedance of the source and load perfectly match the characteristic impedance of the line (Zs = ZL = Z0), maximum power is transferred, and reflections are minimized. Mismatches lead to signal distortion and power loss.
For example, a coaxial cable might have a characteristic impedance of 50 ohms, while a twisted-pair transmission line might have a characteristic impedance of 100 ohms. Matching the impedance of your equipment (e.g., a transmitter and receiver) to these values is crucial for optimal signal integrity.
Q 2. Derive the transmission line equations and explain their implications.
The transmission line equations describe the voltage (V) and current (I) along a transmission line as a function of distance (x) and time (t). They are derived from Maxwell’s equations and are based on the distributed parameters of the line: resistance (R), inductance (L), conductance (G), and capacitance (C) per unit length.
The equations are:
∂V/∂x = - (R + jωL)I
∂I/∂x = - (G + jωC)V
where j is the imaginary unit and ω is the angular frequency.
These equations show how the voltage and current waves propagate along the line. Solving these equations yields expressions for voltage and current as a sum of forward and backward traveling waves, highlighting the importance of impedance matching to minimize reflections.
The implications are far-reaching. These equations are crucial for predicting signal attenuation, propagation speed, reflection coefficients, and ultimately, the overall performance of a transmission line in various applications, from high-frequency communication systems to power distribution networks.
Q 3. What are the different types of transmission lines and their applications?
Transmission lines come in various types, each suited for different applications based on their frequency range, impedance, and physical characteristics.
- Coaxial Cables: Consist of a central conductor surrounded by an insulator and an outer conductor, providing excellent shielding and are widely used in high-frequency applications like cable television, radio frequency (RF) communication, and instrumentation.
- Twisted-Pair Cables: Two insulated conductors twisted together to reduce electromagnetic interference (EMI). Commonly used in telecommunications and local area networks (LANs).
- Microstrip Lines: A printed circuit board (PCB) based transmission line consisting of a conductor above a ground plane, separated by a dielectric substrate. Used extensively in microwave integrated circuits (MICs).
- Stripline: Similar to microstrip but with the conductor embedded within a dielectric substrate between two ground planes. Offers better shielding than microstrip.
- Parallel-Wire Lines: Two parallel conductors separated by a dielectric. Simpler to construct but less effective shielding than coaxial cables. Used in some older applications.
The choice of transmission line depends on factors such as frequency, power handling capability, cost, and desired level of signal integrity. For instance, coaxial cables are preferred for high-frequency applications requiring excellent shielding, while twisted-pair lines are cost-effective for lower frequency applications where shielding requirements are less stringent.
Q 4. Describe the phenomena of reflection and standing waves on a transmission line.
Reflections and standing waves arise when there’s impedance mismatch at the termination of a transmission line. When a wave encounters an impedance discontinuity (e.g., a load impedance different from the characteristic impedance), part of the wave is reflected back towards the source.
Reflection: The reflected wave interferes with the incident wave, resulting in a superposition of waves traveling in opposite directions. The amount of reflection is quantified by the reflection coefficient (Γ).
Standing Waves: The interference between incident and reflected waves creates standing waves, characterized by points of maximum voltage (antinodes) and minimum voltage (nodes). These standing waves indicate impedance mismatch and can lead to power loss and signal distortion. Imagine a rope fixed at one end; plucking it creates standing waves, similar to how reflections create standing waves on a mismatched transmission line.
For instance, if a 50-ohm transmission line is terminated with a 100-ohm load, a significant portion of the signal will be reflected, creating standing waves and reducing the power delivered to the load.
Q 5. Explain the concept of impedance matching and its importance in transmission line design.
Impedance matching is the technique of ensuring that the impedance of the source, transmission line, and load are all equal. This is crucial for maximizing power transfer and minimizing signal reflections. When the impedances are matched, the incident wave is completely absorbed by the load, resulting in no reflected wave.
The importance of impedance matching is paramount in efficient system design. Mismatches lead to signal attenuation, distortion, and even damage to equipment. In RF systems, for example, mismatches can lead to significant power loss, hindering communication. In high-power applications, mismatches can generate excessive heat, potentially causing equipment failure.
Impedance matching can be achieved using various techniques, including using matching networks (e.g., L-sections, pi-networks), impedance transformers (e.g., quarter-wavelength transformers), and attenuators.
Q 6. How do you calculate the voltage standing wave ratio (VSWR)?
The Voltage Standing Wave Ratio (VSWR) is a dimensionless quantity that quantifies the severity of impedance mismatches on a transmission line. It’s defined as the ratio of the maximum voltage to the minimum voltage along the line.
VSWR = Vmax / Vmin
It’s also related to the reflection coefficient (Γ) by:
VSWR = (1 + |Γ|) / (1 – |Γ|)
A VSWR of 1 indicates a perfect match (no reflections), while a higher VSWR indicates a greater mismatch and more significant reflections. For example, a VSWR of 2 indicates a significant mismatch, while a VSWR closer to 1 indicates a good impedance match. VSWR is a key parameter used to assess the quality of transmission line installations and equipment.
Q 7. Explain the Smith Chart and its use in transmission line analysis and design.
The Smith Chart is a graphical tool used for analyzing and designing transmission line circuits. It’s a polar plot that represents complex impedance (or admittance) in a normalized form. This normalization simplifies calculations and allows for easy visualization of impedance transformations.
The chart provides a convenient way to determine reflection coefficients, impedance transformations, and the locations of matching networks. It’s particularly useful for solving problems involving impedance mismatches, designing matching networks, and analyzing standing wave patterns.
For instance, you can use a Smith chart to find the location of a shunt capacitor needed to match a specific load impedance to a transmission line. It is widely used in RF engineering and microwave design to optimize transmission line performance and system efficiency. It simplifies complex calculations by providing a visual representation of impedance transformations, reflection coefficients, and other important parameters.
Q 8. What are the different types of terminations used in transmission lines and their effects?
Transmission line terminations describe how the line ends. The type of termination significantly impacts signal reflection and overall performance. Improper termination can lead to signal distortion and power loss.
- Open Circuit: The line ends without a connection. This results in total reflection of the signal, causing significant signal distortion and potential damage to the source.
- Short Circuit: The line ends with a direct connection. This also leads to total reflection, but with a 180-degree phase shift. Again, distortion is a major issue.
- Matched Termination (or Characteristic Impedance): The line is terminated with a resistor equal to its characteristic impedance (Z0). This prevents reflections, ensuring maximum power transfer and minimal signal distortion. Think of it like a perfectly smooth transition – the signal flows seamlessly through the termination.
- Mismatched Termination: Any termination that is not equal to Z0. This will result in partial reflections, leading to standing waves and signal degradation. The amount of reflection depends on the degree of mismatch.
Example: In a high-frequency communication system, a matched termination is crucial. Without it, reflections can cause interference, echoes, and data errors. Imagine trying to send a message through a rope – an abrupt end (open circuit) will make the message bounce back, whereas a smoothly attached weight (matched termination) will ensure the message goes through cleanly.
Q 9. Describe the concept of distributed parameters in transmission lines.
Unlike lumped element circuits where components are assumed to be concentrated at specific points, transmission lines have distributed parameters. This means the inductance (L), capacitance (C), resistance (R), and conductance (G) are uniformly distributed along the entire length of the line. Each infinitesimally small segment of the line possesses these parameters.
This distribution is crucial because at high frequencies, the assumption of lumped elements breaks down. The physical length of the components becomes comparable to the wavelength of the signal, leading to significant phase shifts and signal distortion. Distributed parameter models accurately account for these effects.
Imagine a garden hose – the water pressure (voltage) and flow (current) aren’t concentrated at specific points but are distributed along the entire length. Similarly, the properties of a transmission line are spread along its length.
Q 10. Explain the difference between lossless and lossy transmission lines.
The key difference lies in the presence of losses.
- Lossless Transmission Line: A theoretical model where the resistance (R) and conductance (G) are zero. This means there are no energy losses due to resistive heating in the conductors or leakage currents through the insulation. While not physically realizable, it’s a useful simplification for initial analysis.
- Lossy Transmission Line: A more realistic model where R and G are non-zero. This accounts for energy loss as heat in the conductors and leakage currents through the dielectric material surrounding the conductors. The losses attenuate the signal as it travels along the line.
Practical Implications: Lossless models simplify calculations but can give misleading results, particularly for long lines or high frequencies. Lossy models offer greater accuracy but require more complex analysis. The choice depends on the application and desired accuracy level. For short lines at lower frequencies, a lossless approximation might suffice. However, for long high-frequency lines, like submarine cables or long-distance power transmission, a lossy model is essential.
Q 11. How do you model a transmission line using lumped element circuits?
Modeling a transmission line using lumped elements involves dividing the line into many small sections, each represented by a simple equivalent circuit. Each section contains a series impedance (RΔz + jωLΔz) and a shunt admittance (GΔz + jωCΔz), where Δz is the length of the section. By cascading many such sections, we can approximate the behavior of the distributed line.
This approach is particularly useful for computer simulations where we can iteratively increase the number of sections to improve accuracy. However, it’s important to note that this model is an approximation; the accuracy depends on the number of sections used. The more sections, the better the approximation, but also the more computationally intensive it becomes.
The lumped element model provides a good understanding of the fundamental transmission line behavior but it falls short of capturing the nuances of high-frequency behavior compared to the full distributed parameter analysis.
Q 12. What are the different methods for measuring transmission line parameters?
Measuring transmission line parameters (R, L, C, G) often involves using specialized techniques and equipment. Common methods include:
- Time Domain Reflectometry (TDR): A pulse is sent down the line, and the reflections are analyzed to determine impedance mismatches and locate faults. This indirectly reveals information about the line parameters.
- Frequency Domain Methods: Using a network analyzer, we can measure the input impedance of the line at various frequencies. This data can then be used to extract the distributed parameters using curve-fitting techniques or analytical models. This is a very common method for characterizing high-frequency transmission lines.
- Direct Measurement: For some lines, it might be possible to measure R, L, and C directly using techniques like inductance bridges, capacitance meters, and resistance measurements. However, measuring G is typically more challenging.
The choice of method depends on the frequency range of operation, the line’s physical characteristics, and the desired accuracy.
Q 13. Explain the concept of propagation constant and its components.
The propagation constant (γ) describes how a wave propagates along a transmission line. It’s a complex quantity, having two components:
- Attenuation Constant (α): Represents the loss of signal amplitude as the wave travels along the line (measured in nepers/meter). It accounts for energy loss due to resistance and conductance.
- Phase Constant (β): Represents the change in phase of the wave as it travels along the line (measured in radians/meter). It reflects the time delay and phase shift experienced by the signal as it travels.
The propagation constant is given by: γ = α + jβ = √[(R + jωL)(G + jωC)]
Therefore, the attenuation constant describes the signal’s decay, and the phase constant governs its speed and phase shift along the transmission line.
Q 14. How does frequency affect the performance of a transmission line?
Frequency significantly affects transmission line performance. As frequency increases:
- Increased Attenuation: The skin effect causes higher current concentration near the conductor surface, increasing resistance (R) and hence attenuation (α). Similarly, the capacitive and inductive reactances change, further influencing the propagation constant.
- Wavelength Changes: The wavelength (λ) decreases as frequency increases (λ = v/f, where v is the velocity of propagation). This makes the line electrically longer at higher frequencies. This is critical in determining whether a line can be considered electrically short or long.
- Increased Dispersion: Different frequency components of a signal travel at slightly different speeds due to frequency dependence of phase velocity, resulting in signal distortion. This is particularly important for wideband signals.
- Resonance and Anti-resonance Effects: At specific frequencies, depending on the line length and termination, resonances and anti-resonances can occur. These can lead to significant amplification or attenuation of certain frequencies.
Example: High-frequency signals in a coaxial cable experience greater attenuation than low-frequency signals. In designing high-speed digital circuits, frequency effects must be carefully considered to ensure signal integrity.
Q 15. What are the effects of skin effect on transmission lines?
The skin effect is a phenomenon where alternating current (AC) tends to concentrate near the surface of a conductor, rather than flowing uniformly throughout its cross-section. This is due to the opposing magnetic fields induced by the changing current. The higher the frequency, the more pronounced the skin effect.
On transmission lines, the skin effect leads to several crucial consequences:
- Increased AC resistance: The effective cross-sectional area for current flow is reduced, leading to a higher resistance than the DC resistance. This results in increased power loss in the transmission line (I²R losses).
- Reduced current-carrying capacity: The smaller effective area means the line can’t carry as much current as it could with a uniform current distribution.
- Increased inductance: The non-uniform current distribution also alters the inductance of the line, potentially affecting its impedance and causing further complications in line design and performance.
Consider a high-voltage power transmission line operating at 50Hz. The skin effect will significantly impact its resistance, necessitating the use of larger conductors or special designs like bundled conductors to mitigate the losses. At higher frequencies, like those used in communication systems, the skin effect is even more dominant, requiring careful conductor selection and design.
Career Expert Tips:
- Ace those interviews! Prepare effectively by reviewing the Top 50 Most Common Interview Questions on ResumeGemini.
- Navigate your job search with confidence! Explore a wide range of Career Tips on ResumeGemini. Learn about common challenges and recommendations to overcome them.
- Craft the perfect resume! Master the Art of Resume Writing with ResumeGemini’s guide. Showcase your unique qualifications and achievements effectively.
- Don’t miss out on holiday savings! Build your dream resume with ResumeGemini’s ATS optimized templates.
Q 16. How do you design a transmission line for a specific application?
Designing a transmission line for a specific application requires a systematic approach, considering several critical factors:
- Frequency of operation: This dictates the conductor size, spacing, and dielectric properties to minimize signal attenuation and distortion.
- Power level: The required power transfer capacity influences conductor size and material selection to handle the current without excessive heating and voltage drop.
- Length of the line: Longer lines necessitate more careful impedance matching to avoid reflections and signal loss.
- Transmission medium: Different mediums (coaxial cable, twisted pair, waveguide, free space) have unique characteristics affecting signal propagation.
- Environmental conditions: Factors like temperature, humidity, and surrounding objects impact performance and require appropriate insulation and shielding.
For example, designing a high-frequency communication line requires a different approach than designing a long-distance power transmission line. The former would likely utilize coaxial cable with careful impedance matching, whereas the latter would use overhead conductors with considerations for sag, wind loading, and minimizing corona effects. Detailed simulations and modelling are often necessary to optimize the design.
Q 17. Explain the concept of impedance transformation using transmission lines.
Impedance transformation using transmission lines involves changing the characteristic impedance (Z0) of a line to match the impedance of the source and load, thereby maximizing power transfer and minimizing reflections. This is achieved by carefully selecting the length and characteristic impedance of the transmission line.
Quarter-wave transformers are a common method. A transmission line with a length of a quarter-wavelength (λ/4) and a characteristic impedance (Zt) can transform an impedance ZL at its output to an impedance Zs at its input, according to the formula:
Zs = Z0²/ZL
where Z0 = √(ZsZL)
For instance, if you want to match a 50-ohm load to a 100-ohm source, you would need a quarter-wave transformer with a characteristic impedance of 70.7 ohms (√(50*100)). This technique is crucial in microwave circuits and high-frequency applications where impedance matching is essential for optimal performance.
Q 18. What are the different types of transmission line faults and how are they analyzed?
Transmission line faults can be broadly classified into:
- Three-phase faults: All three phases are simultaneously short-circuited. These are usually the most severe faults.
- Line-to-line faults: Two phases are short-circuited.
- Line-to-ground faults: One phase is short-circuited to ground. This is a common type of fault.
Fault analysis involves determining the fault current, fault location, and its impact on the system. This is typically done using symmetrical component analysis. This involves transforming the unbalanced fault currents into symmetrical components (positive, negative, and zero sequence components), simplifying the analysis. The fault location can be identified using techniques such as distance protection relays, which measure the impedance seen from the relay location to the fault.
The analysis helps in the design of protective relaying schemes, ensuring rapid fault clearing and minimizing damage to the system and equipment.
Q 19. How do you analyze transient phenomena on transmission lines?
Analyzing transient phenomena on transmission lines involves studying the behavior of the line under sudden changes, such as switching operations, lightning strikes, or faults. These transients can lead to high voltage surges and oscillations, potentially damaging equipment.
The most common method is using the traveling wave method, which considers the propagation of voltage and current waves along the line. These waves travel at the speed of light in the medium and are reflected at discontinuities (e.g., open ends, short circuits, junctions). Simulation software using numerical techniques like the finite difference time-domain (FDTD) method is often employed to analyze complex transient behavior.
Understanding these transients is crucial for designing surge arresters, insulators, and other protective devices to mitigate the harmful effects of voltage surges and oscillations. For example, lightning strikes can generate extremely high voltage transients, necessitating the installation of lightning arresters to divert the surge current to the ground.
Q 20. Explain the concept of surge impedance loading (SIL).
Surge impedance loading (SIL) is the power load that a transmission line can carry without causing any reflections. It’s the power that is completely absorbed by the line’s characteristic impedance, resulting in a purely resistive load. At SIL, the voltage and current profiles along the line are uniform.
SIL is calculated as:
SIL = V²/Z0
where V is the line-to-line voltage and Z0 is the surge impedance of the line. For example, a 220 kV line with a surge impedance of 400 ohms will have an SIL of approximately 121 MW.
Understanding SIL is vital in transmission line planning and operation. Operating close to SIL minimizes voltage fluctuations and power oscillations. However, exceeding SIL can lead to voltage instability and significant power oscillations.
Q 21. What are the different methods for compensating for transmission line losses?
Transmission line losses can be compensated using several methods:
- Series compensation: This involves installing series capacitors along the line to reduce the line reactance and improve voltage regulation. Series compensation reduces the voltage drop along the line, especially under heavy loading conditions.
- Shunt compensation: This involves installing shunt reactors or capacitors to control the line’s reactive power flow. Shunt capacitors are used to compensate for inductive reactance, improving power factor and voltage profile.
- Static Synchronous Compensators (STATCOMs) and Static Synchronous Series Compensators (SSSC): These are advanced power electronic devices that provide flexible and dynamic reactive power compensation, offering improved voltage regulation and power flow control compared to conventional shunt and series compensation.
- High-temperature low-sag (HTLS) conductors: These conductors have superior electrical and mechanical properties, leading to reduced resistance and sag, resulting in lower losses.
The choice of compensation method depends on factors such as the line length, power level, voltage level, and cost considerations. For long transmission lines, a combination of series and shunt compensation might be necessary to achieve optimal performance.
Q 22. Describe the different types of insulators used in transmission line construction.
Transmission line insulators are crucial components that prevent current leakage to the ground and protect the line from short circuits. They’re designed to withstand high voltages and environmental stresses. Several types exist, each suited to different applications:
- Pin Insulators: These are the simplest type, consisting of a porcelain or glass insulator with a pin at the top for conductor attachment and a groove at the bottom for mounting on a cross-arm. They are cost-effective but have limited voltage capabilities. Imagine them as simple, sturdy ceramic supports holding the power line.
- Suspension Insulators: These are a string of individual disc insulators connected in series. This configuration allows for higher voltage applications as the voltage is distributed across multiple units. Think of them as a chain of ceramic links, each sharing the load and increasing overall strength. They’re commonly used in high-voltage transmission lines.
- Strain Insulators: Used at points of high tension in the line, such as towers, these insulators are stronger than suspension insulators to withstand the extra stress. They’re designed to handle the extra mechanical pull.
- Post Insulators: These are typically used in substations and areas with higher pollution levels. They have a more compact design than pin insulators and are better at shedding dirt and moisture. Think of them as a more robust and weather-resistant pin insulator.
The choice of insulator depends on factors such as voltage level, environmental conditions (pollution, humidity), and mechanical strength requirements.
Q 23. Explain the importance of grounding in transmission line systems.
Grounding in transmission line systems is absolutely vital for safety and reliable operation. It serves several crucial purposes:
- Protection against Lightning Strikes: A properly grounded system provides a low-resistance path for lightning current to flow into the earth, preventing damage to equipment and ensuring personnel safety. Imagine a lightning rod – grounding provides a similar protective pathway.
- Fault Current Limitation: During a fault (e.g., a short circuit), grounding quickly diverts the fault current to the earth, limiting the voltage surge and preventing damage to the transmission line and connected equipment. This is akin to having a safety valve in a pressure system.
- Voltage Stabilization: Grounding helps maintain a stable voltage level by providing a reference point for the electrical system. This ensures consistent power delivery.
- Personnel Safety: Grounding prevents dangerous voltage buildup on the transmission line structures, reducing the risk of electric shock. Think of it as creating a safe operational environment.
Grounding is achieved through the use of ground wires, grounding rods, and connection to the earth. The effectiveness of the grounding system depends on the resistivity of the soil and the quality of the connections.
Q 24. How are transmission line sag and tension calculated?
Calculating transmission line sag and tension is crucial for ensuring line stability and preventing conductor breakage. Sag is the vertical distance between the conductor and its lowest point, while tension is the force in the conductor. These calculations consider several factors:
- Conductor weight (w): Weight per unit length of the conductor.
- Span length (L): The horizontal distance between two supports.
- Temperature (T): Affects conductor length and sag.
- Coefficient of linear expansion (α): Describes how much the conductor expands with temperature changes.
- Elastic modulus (E): Measures the conductor’s stiffness.
Several methods are employed. The simplest assumes a parabolic curve for the conductor’s sag, which is a good approximation for small sag-to-span ratios:
Sag (S) ≈ (wL²)/(8T)
More accurate methods utilize hyperbolic functions to account for larger sag-to-span ratios. Software tools and iterative techniques are often used for complex calculations, particularly when considering varying terrain and ice loading. The tension is often determined from the sag and the conductor’s properties. The process involves balancing the need for low sag (for ground clearance) with acceptable conductor tension (to prevent breakage). Incorrect estimations can lead to conductor failure or issues with ground clearance.
Q 25. Explain the different types of transmission line configurations (e.g., single-circuit, double-circuit).
Transmission line configurations dictate how conductors are arranged on towers. Different configurations offer varying capacity and redundancy. Common configurations include:
- Single-circuit lines: These have one circuit per tower, which is the simplest and most economical option for lower power transmission needs. Think of it as a single lane highway.
- Double-circuit lines: Two circuits are mounted on the same tower, typically to increase transmission capacity. This configuration is common for higher power needs, like a two-lane highway.
- Twin-circuit lines: Two single-circuit lines run parallel, usually spaced to minimise inductive coupling. Often seen when increasing capacity is not possible by simply adding conductors to one tower, and multiple circuits are necessary.
- Bundled conductors: Multiple conductors are grouped together to increase the transmission capacity and reduce corona loss. This is like having multiple thinner wires running side by side, resulting in greater capacity and lower energy loss.
The choice of configuration depends on factors like power requirements, right-of-way constraints, cost considerations, and reliability requirements.
Q 26. Describe the role of power transformers in transmission systems.
Power transformers are essential in transmission systems, primarily for stepping up and stepping down voltage levels. They act as voltage converters.
- Step-up transformers: These transformers increase voltage at generating stations, reducing transmission losses and allowing for efficient power transfer over long distances. Higher voltage means lower current for the same power, resulting in reduced losses. Imagine a funnel; the wide end is the high-voltage transmission line, and the narrow end is the lower voltage at the generation station.
- Step-down transformers: These reduce voltage at substations and distribution points to levels suitable for industrial, commercial, and residential use. This safely lowers the voltage from transmission levels to safe levels.
Transformers are critical for matching voltage levels between different parts of the power grid, ensuring efficient and safe power delivery. They are large and expensive, requiring substantial investment but are pivotal to the functionality of the whole system.
Q 27. What are the environmental considerations in transmission line design and construction?
Environmental considerations are increasingly important in transmission line design and construction. Key aspects include:
- Visual impact: Minimising the visual intrusion of transmission lines on landscapes and communities is crucial. This often involves careful route selection and using strategies such as undergrounding lines or employing aesthetically pleasing tower designs.
- Right-of-way management: Minimizing the land area used for transmission lines and their impact on ecosystems is essential, including preserving wildlife habitats and minimizing habitat fragmentation.
- Electromagnetic fields (EMF): Concerns exist regarding potential health effects from EMF generated by transmission lines. Mitigation strategies involve careful planning and design to minimise field strength within populated areas.
- Noise pollution: Corona effect can generate audible noise, particularly during wet weather. Bundled conductors and careful conductor design can minimize noise levels.
- Impact on birds and wildlife: Collisions with transmission lines are a concern for birds. Mitigation techniques include marking conductors and towers to improve visibility.
Environmental impact assessments are typically required before transmission line projects commence. Balancing the need for reliable power delivery with environmental protection is a key challenge in transmission line design and construction.
Key Topics to Learn for Transmission Line Theory Interview
- Transmission Line Parameters: Understand the concepts of resistance, inductance, capacitance, and conductance per unit length, and their impact on line performance. Learn how to calculate these parameters for different line configurations.
- Wave Propagation: Grasp the principles of wave propagation along transmission lines, including reflection and transmission coefficients, standing waves, and the concept of impedance matching.
- Transmission Line Equations: Become proficient in solving the telegrapher’s equations and applying them to analyze voltage and current distributions along the line under various conditions (e.g., open circuit, short circuit, terminated lines).
- Smith Chart: Learn to utilize the Smith chart for impedance matching, reflection coefficient calculation, and analyzing transmission line performance.
- Different Line Types: Familiarize yourself with the characteristics and applications of various transmission line types, such as coaxial cables, microstrip lines, and parallel-wire lines.
- Power Transmission Applications: Understand how Transmission Line Theory is applied in high-voltage power transmission systems, including the design and analysis of long transmission lines and surge protection.
- Signal Integrity: Explore the role of Transmission Line Theory in maintaining signal integrity in high-speed digital circuits and communication systems.
- Practical Problem Solving: Develop your ability to model and solve real-world problems involving transmission lines, using both analytical and numerical methods. Practice deriving relevant equations from first principles.
Next Steps
Mastering Transmission Line Theory is crucial for career advancement in fields like power systems engineering, telecommunications, and high-speed electronics. A strong understanding of these principles demonstrates a solid foundation and opens doors to exciting opportunities. To further enhance your job prospects, creating a compelling and ATS-friendly resume is essential. ResumeGemini is a trusted resource that can help you build a professional resume that highlights your skills and experience effectively. Examples of resumes tailored to Transmission Line Theory are available within ResumeGemini to guide you.
Explore more articles
Users Rating of Our Blogs
Share Your Experience
We value your feedback! Please rate our content and share your thoughts (optional).
What Readers Say About Our Blog
Hi, I’m Jay, we have a few potential clients that are interested in your services, thought you might be a good fit. I’d love to talk about the details, when do you have time to talk?
Best,
Jay
Founder | CEO